예제
2014년 6월에 있었던 제 6대 전국 지방선거에서는 지방 자치 단체장을 선거로 뽑았습니다. 그 당시 JTBC에서는 투표일 직전 현대리서치와 오베이에게 의뢰하여 투표 의향과 지지 후보를 물어보았고 그 결과는 경기도의 경우 다음과 같았습니다.
| 구역 | 유효 표본수 | 남경필 지지 (%) | 김진표 지지 (%) | 구역 | 유효 표본수 | 남경필 지지 (%) | 김진표 지지 (%) |
|---|---|---|---|---|---|---|---|
| 과천/군표/의왕 | 60 | 53.8 | 41.7 | 평택 | 55 | 53.8 | 46.2 |
| 성남 | 129 | 56.6 | 43.4 | 화성 | 53 | 45.5 | 54.5 |
| 수원 | 152 | 53.4 | 46.6 | 고양 | 138 | 45.2 | 54.8 |
| 안성/용인 | 106 | 43.6 | 56.4 | 김포 | 40 | 48.2 | 51.8 |
| 안양 | 81 | 63.8 | 36.2 | 파주 | 38 | 24.5 | 75.5 |
| 광명 | 39 | 23.4 | 76.6 | 동두천/양주/포천/연천 | 42 | 68.9 | 31.1 |
| 부천 | 104 | 53.6 | 46.4 | 의정부 | 55 | 36.6 | 63.4 |
| 시흥 | 41 | 41.9 | 58.1 | 가평/양평/여주/이천 | 53 | 66.2 | 33.8 |
| 안산 | 79 | 50.5 | 49.5 | 광주/구리/하남 | 71 | 39.5 | 60.5 |
| 오산 | 32 | 41.4 | 58.6 | 남양주 | 71 | 42.7 | 57.3 |
위 자료를 이용한 선거 예측의 정확성을 높혀주기 위해서 2년전에 있었던 대선 투표 결과를 사전정보로 반영한 베이즈 추정을 구현하는것이 하나의 방법일수 있습니다. 어떻게 하면 될까요?
풀이
이 문제는 전형적인 베이즈 추정 문제입니다. 각 구역 $i$에서의 참값을 $Y_i$라고 하면 그에 대한 통계 추정량값은 $\hat{Y}_i$으로표현될수 있습니다. 그리고 2년전 대선에서 그 지역의 참값 (새누리당 대선후보 투표율)을 $X_i$라고 하면 $Y_i$ 와 $X_i$이 어느 정도 상관관계가 있을 것이라고 생각할수 있습니다. 이러한 관계는 일종의 사전모형이 될 것입니다. 즉, 사전모형이란 현재 자료수집 이전의 정보에 대한 모형으로 이 경우에는 \begin{equation} Y_i = \gamma X_i + e_i , \ \ \ e_i \sim N( 0, X_i \sigma^2) \ \ \ (1) \end{equation} 으로 표현할수 있고 이 경우 $\gamma$와 $\sigma^2$은 사전모형에 대한 모수가 됩니다.
다음으로는 현재 자료를 통해서 얻어지는 통계량의 모형을 구해야 합니다. 이 경우에는 \begin{equation} \hat{Y}_i\mid Y_i \sim N( Y_i , V_i) \ \ \ \ \ \ (2) \end{equation} 으로 표현될수 있고 $V_i$는 $\hat{Y}_i$의 분산값으로써 위의 경우에는 $(1- \hat{Y}_i)\hat{Y}_i/ n_i$으로 계산될 수 있습니다.
위의 두 식을 결합하면 베이즈 정리를 이용하여 사후 모형이 다음과 같이 얻어집니다. \begin{equation} Y_i \mid ( X_i , \hat{Y}_i ) \sim N [ \alpha_i \hat{Y}_i + (1-\alpha_i) \gamma X_i, (1-\alpha_i) X_i \sigma^2 ] \ \ \ \ \ \ \ \ (3) \end{equation} 이때 으로 계산됩니다. 이렇게 얻어진 사후 모형의 조건부 기대값 \begin{equation} \hat{Y}_i^* \equiv E ( Y_i \mid X_i , \hat{Y}_i ) = \alpha_i \hat{Y}_i + (1-\alpha_i) \gamma X_i \end{equation} 은 서베이 결과와 과거 대선 결과를 반영하는 예측으로써 사전 모형의 유용성 정도에 따라 예측의 정확성을 높여주는 효과를 가져옵니다. 위의 조건부 기대값 $\hat{Y}_i^*$이 베이즈 추정량이라고도 부르는데 실제로는 이 베이즈 추정량이 사전모형 모수의 함수이므로 이를 추정하여 대입해서 계산해야 합니다.
토론
-
위의 예에서 (3)의 사후 모형이 정규분포로 얻어진 것은 (1)의 사전 모형도 정규분포이고 (2)의 관측치 모형도 정규 분포를 따르기 때문입니다. (엄밀하게 말하면 (2)는 추정량의 표본분포입니다. ) 만약 (1)의 사전 모형이 정규 분포가 아닌 다른 모형이면 사후 분포는 정규 분포를 따르지 않고 \begin{equation} p(Y_i \mid \hat{Y}_i, X_i) = \frac{ f( \hat{Y}_i \mid Y_i) \pi (Y_i \mid X_i)}{ \int f( \hat{Y}_i \mid Y_i) \pi (Y_i \mid X_i) d Y_i} \end{equation} 를 따르게 됩니다. 이러한 사후 분포가 형태가 알려져 있지 않은 경우에는 몬테카를로 방법을 사용해서 베이즈 추정량을 계산합니다.
-
모수 추정은 EM 알고리즘이나 베이지안 MCMC 방법을 사용합니다. 만약 EM 알고리즘을 사용하는 경우에는 모수 $\gamma$와 $\sigma^2$에 대한 score equation 을 $Y_i$와 $Y_i^2$의 함수로 표현한 후에 모형 (3)에서 얻어진 사후 기대값을 계산해서 반복적으로 풀어야 합니다. (디테일은 생략하겠습니다) 또는 (1)과 (2)를 결합하여 \begin{equation} \hat{Y}_i \sim N[X_i \gamma , V_i + X_i \sigma^2 ] \end{equation} 을 얻을수 있으므로 $(X_i , \hat{Y}_i)$의 관측치를 바탕으로 최대우도 추정법을 이용하여 모수를 추정할 수 있습니다. 이렇게 모수를 최대우도 추정으로 계산한후 $\hat{Y}_i^*$ 에 대입해서 구하는 것을 Empirical Bayes 추정이라고 합니다.
-
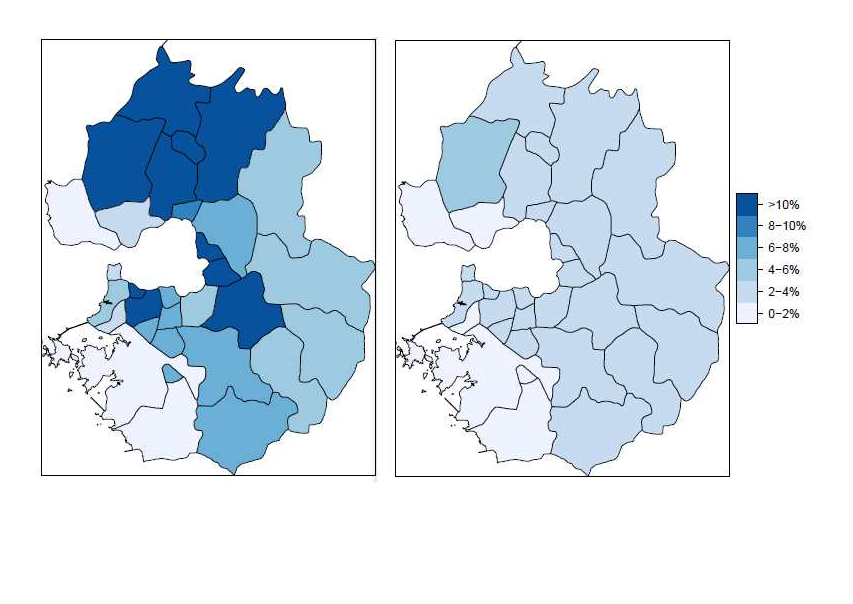
아래 그림은 위의 방법으로 예측한 결과를 실제 투표 결과와 비교한 오차 절대값의 분포입니다. 왼쪽은 서베이 결과만을 사용한 예측 분석의 오차 분포이고 오른쪽은 서베이 결과와 대선자료를 베이즈 추정으로 결합한 예측 분석의 오차 분포입니다. 서베이 결과는 평균 7% 의 오차를 보여주었는데 베이즈 추정은 평균 2%의 오차를 보여주었습니다. 이 경우 베이즈 추정으로 정확도가 상당히 개선되었다고 이야기 할수 있을 것입니다.
. .