예제
몬티홀(Monty Hall) 문제를 들어보셨나요? 몬티홀 문제는 미국의 어느 방송국에서 했던 “Let’s Make a Deal”이라는 쇼 프로그램에서 진행자 Monty Hall 씨의 이름을 따서 붙혀진 흥미로운 게임입니다. 이 게임은 다음과 같이 진행됩니다.
-
방송국 스튜디오에는 3개의 문이 닫힌채로 보여집니다. 그 문 뒤에는 각각 2개의 염소와 1개의 멋진 스포츠카가 임의의 순서대로 배치되어 있습니다. 주인공이 하나의 문을 선택하게 되는데 이 스포츠카가 있는 문을 선택하면 그 차를 갖게 되는 쇼입니다.
-
먼저 이 프로그램에서는 주인공이 나와서 문을 하나 고릅니다. (예를 들어 첫번째 문을 골랐다고 합시다)
-
그러면 그 프로그램의 진행자인 몬티 홀씨는 어느 문 뒤에 스포츠카가 있는지를 알기에 나머지 두 문 중에서 염소가 있는 문을 열어 보여 줍니다. (만약 문 1에 자동차가 있으면 문2와 문3중에서 하나를 임의로 선택해서 보여줍니다.) 그리고는 주인공에게 묻습니다. “당신은 처음의 선택을 바꾸겠습니까?” 하고 말입니다. 주인공은 처음의 선택한 문을 고르거나 아니면 나머지 남은 문을 고르거나를 결정해야 합니다.
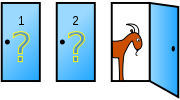
주인공은 처음의 선택을 바꾸는게 나을까요? 아니면 둘다 마찬가지 인가요?
풀이
이 문제는 조건부 확률의 개념을 설명하는데 흔히 사용되는 사례입니다. 아무런 정보가 없을때에는 자동차가 특정 문 뒤에 있을 확률은 각각 1/3입니다. 즉, C1 을 첫번째 문에 자동차를 놓는 사건, C2 를 두번째 문에 자동차를 놓는 사건, C3 를 세번째 문에 자동차를 놓는 사건으로 한다면 P(C1)=P(C2)=P(C3)=1/3 입니다.
그런데 여기에 새로운 정보가 들어갑니다. 몬티홀씨의 행동은 어느 문에 자동차가 있는지에 대한 정보를 제공합니다. 주인공이 처음에 문 1을 선택했을때, D1 을 몬티홀씨가 첫번째 문을 보여주는 사건, D2 을 몬티홀씨가 두번째 문을 보여주는 사건, D3을 몬티홀씨가 세번째 문을 보여주는 사건이라고 정의한다면 몬티홀씨의 행동은 참값에 따라 다르게 결정되므로 다음과 같은 조건부 확률을 갖게 됩니다. 즉, 자동차가 첫번째 문에 있다면 문2 와 문3에 둘다 염소가 있으므로 몬티홀씨는 두 문중에 하나를 같은 확률로 뽑아 보여줍니다. 하지만 자동차가 두번째 문에 있다면 나머지 두 문중에 염소가 있는 문은 문3 뿐입니다. 그래서 $P(D3 | C2)= 1$이 되는 것입니다. 마찬가지로 생각하면 자동차가 세번째 문에 있으면 $P(D3 | C3)= 0$이 됩니다.
따라서 만약 몬티홀씨가 세번째 문을 열었다면 조건부 확률의 정의를 이용하면 으로 계산됩니다. 하지만 이므로 문2에 자동차가 있을 확률이 더 높아집니다. 만약 몬티홀씨가 두번째 문을 열었다면 마찬가지 방법으로 $P(C1 \mid D2)=1/3$이고 $P(C3 \mid D2)=2/3$임을 계산할수 있습니다. 따라서 주인공은 자신의 선택을 바꾸는 것이 항상 유리합니다.
토론
-
문 1에 자동차가 있을 확률은 몬티홀씨의 행위에 상관없이 1/3 로 일정합니다. 그런데 나머지 문에 자동차가 있을 확률은 몬티홀씨의 행위에 영향을 받습니다. 왜냐하면 몬티홀씨는 나머지 두개의 문 중에서 어느 문에 자동차가 없는지를 보여줌으로써 확률을 한쪽으로 몰아주었기 때문입니다. 즉, 처음 확률 1/3 의 확률로 문2 와 문 3에 각각 자동차가 있을수 있었는데 몬티홀씨가 문 3을 열어서 자동차가 없음을 보여주게 되면 그 사건을 통해 문3에 자동차가 있을 확률은 0 이 되고 따라서 문2에 자동차가 있을 확률은 2/3가 되는 것입니다.
-
만약 문이 10개 있다고 하고 주인공이 문 1을 선택했을때 몬티홀씨가 자동차가 없는 나머지 8개 문을 열어서 확인시켜 준다면 이 원리는 더 명확해 집니다.
-
관찰을 통해 확률이 업데이트 되는 것은 학습(learning)의 주요 개념입니다. 위의 예제는 사전확률과 사후확률의 관계로도 표현됩니다. 특정 실험으로부터 어떤 결과가 얻어진다고 할때 그 결과를 얻기 이전에서의 확률은 사전확률이라 불리우고 그 결과를 바탕으로한 조건부 확률은 사후 확률이라고 부릅니다. 사후 확률을 구하는 방법을 베이즈 정리라고 부릅니다. 다음 시간에 좀더 자세히 다루도록 하겠습니다.